

You can use one of these 3 methods to solve quadratic inequalities:ġ. If D 0), based on the 2 real roots obtained from Step 2. Just use mental math to make sure that D > 0. There is no need to calculate the exact value of D. How? Find out if the discriminant D = b^2 - 4ac is positive (> 0).
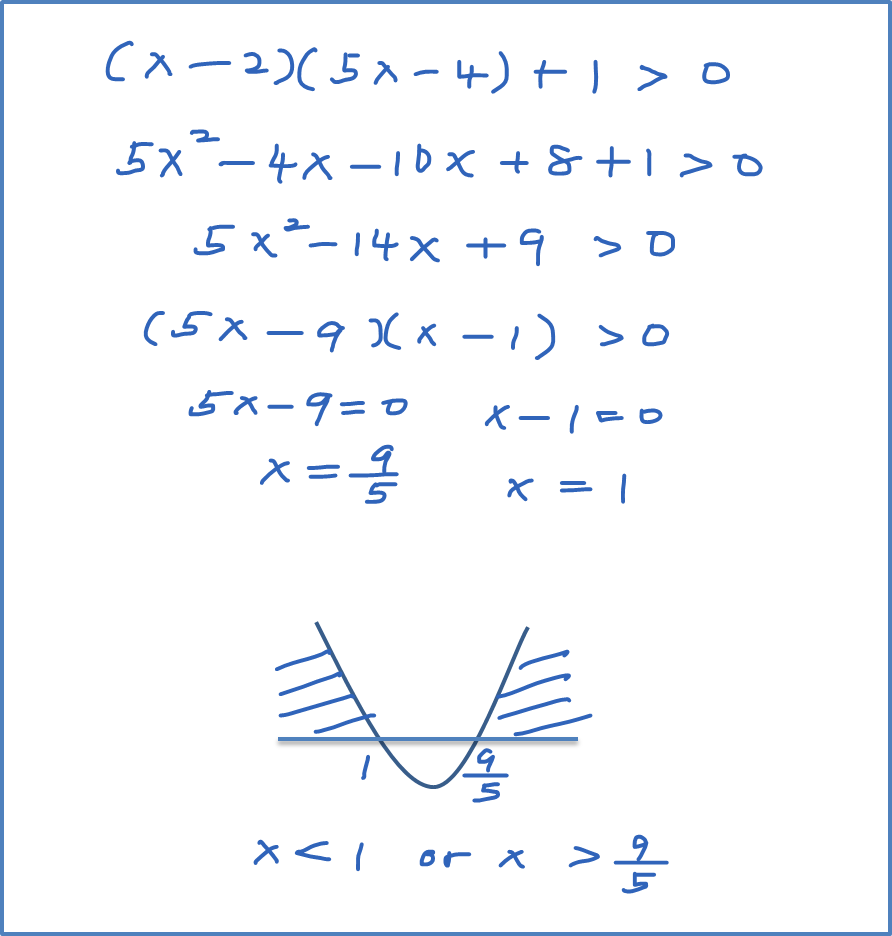
The 4 methods (factoring, completing the square, quadratic formula, and graphing) or the new Diagonal Sum Method (Amazon e-book 2010).īefore proceeding solving, make sure that the quadratic equation has 2 real roots. Solve the quadratic equation f(x) = 0 to get the 2 real roots x1 and x2. In step 1, transform it into standard form f(x) = 3x^2 - 7x - 5 > 0. In Step 1, transform it into standard form: f(x) = 2x^2 + 5x - 7 5. Transform the given inequality into standard form: f(x) = ax^2 + bx + c 0). What is different in the graphing process of an equality and an inequality? How can you check the x-intercepts of a quadratic equation or inequality? Why is it important to test 3 intervals after you have found the critical x values?Īssignment 1.9, 3-24 every 3rd problem, 36-57 every 3rd problem Assignment 1.The standard form of a quadratic inequality in one variable is ax^2 + bx + c > 0 (or 0 8x^2 - 9x - 17 0 (x^2 - 5x + 4x)/(x^2 - 3x - 4) > 0 If true, shade where the point is located. Pick a point not on the parabola and see if it makes a true statement.

SOLUTION First, write and solve the equation obtained by replacing > with =. The graph lies above the x-axis when 4.2 15 algebraically. For what years was the number of teams greater than 100? You want to find the values of xfor which: T(x) > 100 7.51x2 – 16.4x – 65 > 0 Graph y = 7.51x2 – 16.4x – 65 on the domain 0 ≤ x ≤ 9. Robotics The number Tof teams that have participated in a robot-building competition for high school students can be modeled by T(x) = 7.51x2 –16.4x + 35.0, 0 ≤ x ≤ 9 Where x is the number of years since 1992.

STEP 3 Identify the purple regionwhere the two graphs overlap. The graph is the blue region inside (but not including) the parabola y = x2 –2x – 3. The graph is the red region inside and including the parabola y = –x2 + 4. Solving a Quadratic Inequality by Graphing (Looking for x intercepts) x2 − 6x + 5 x2 – 2x – 3 Inequality 2 SOLUTION STEP 1 Graph y ≤ –x2 + 4. Test a point inside the parabola, such as (1, 2000).Ģ000 ≤ 1480 Rappelling continued W≤ 1480d 2 2000≤ 1480(1)2 Because (1, 2000) is not a solution, shade the region below the parabola. Because the inequality symbol is ≤, make the parabola solid. SOLUTION Graph W = 1480d 2 for nonnegative values of d. Rappelling A manila rope used for rappelling down a cliff can safely support a weight W(in pounds) provided W ≤ 1480d 2 where dis the rope’s diameter (in inches). If you get a false statement when you substitute the point into the inequality, shade the opposite area.If you get a true statement when you substitute the point into the inequality, shade that area.Test a point inside the parabola, such as (0, 0).Y > ax2 + bx + c y ≥ ax2 + bx + c y x2 − 2x − 3 x = −b/2a= y = Graphing & Solving Quadratic Inequalities 5.7 What is different in the graphing process of an equality and an inequality? How can you check the x-intercepts of a quadratic equation or inequality? Why is it important to test 3 intervals after you have found the critical x values?


 0 kommentar(er)
0 kommentar(er)
